1.非線性誤差的產生
由于渦街流量計傳感器所測的并不是平均流速,而是漩渦發生體兩側的流速。對于湍流狀態,不同的雷諾數下,流速分布規律是不同的,即不同的流速下具有不同的流速分布,進而說明了渦街流量傳感器檢測到的主要反映漩渦發生體兩側的流速,與管道平均流速的關系不是唯一確定的。這說明渦街流量傳感器的非線性誤差是其檢測機理所決定的。在實際使用時,先繪出傳感器的儀表常數與流體流速的試驗曲線,據此得到不同流速段的實際儀表常數。本文應用MCS-51單片機系列的89C51將試驗曲線事先固化于流量計的EPROM中,用戶結合現場具體工作情況通過鍵盤輸人平均儀表常數Kp的值(Kp=(Kmax+Kmin)/2),實現了渦街傳感器的非線性修正。
2.儀表常數與流體流速的關系及分段補償
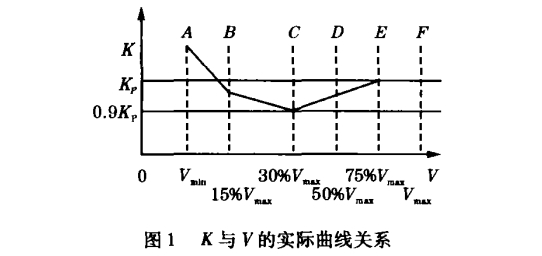
我們知道渦街流量計頻率與流量成正比,理論上講,渦街流量計輸出頻率與流速成正比,也就是說儀表常數恒定。實際上,由于流量計本身的因素導致兩者之間存在一定程度的非線性誤差。鑒此,我們做出了一條儀表常數與流速的實驗關系曲線,如圖1所示。圖中各點坐標分別為A(Vmin,1.0049Kp),
B(15%Vmax,0.997Kp),C(30%Vmax0.992853Kp),D(50%Vmax,0.94883Kp),E(75%Vmax,Kp),F(Vmax,Kp)。
針對這種誤差規律,我們采取分段補償的方式進行誤差修正。由圖1可以看出,隨著流速的降低,曲線偏離平均值越大,對此我們采用的方法可以達到兩個目的:
(1)無論偏差值多大,只要它有規律可循,就可補償修正,還可以把流量的下限即Vmin在坐標上向左移動,即擴大傳感器的量程。
(2)根據精度要求合理劃分區間,在誤差大的低流速區間線段取密一些,在誤差小的高流速區間可適當將區間放寬。
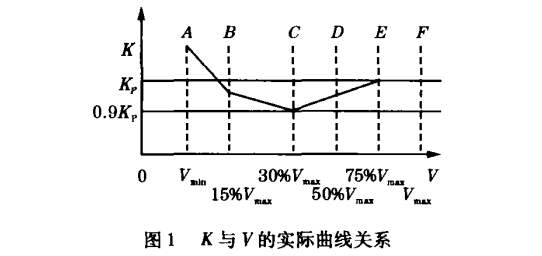
為了滿足修正后非線性誤差在0.3%以下的要求,我們根據理論分析和曲線規律,分別在12%Vmax、60%Vmax處增加兩點(見圖2),坐標分別為G(12%Vmax,Kp),H(60%Vmax,0.998Kp)。理由:①Vmin/Vmax=8%~9%;②DE曲線間無拐點且下凹;③AB曲線間無拐點且下凹。這樣,把整個流速范圍分成了六段,如表1。這樣處理后,可修正非線性誤差在0.3%以下。
3.補償后非線性誤差計算及驗證
表2為補償后各段儀表常數的非線性誤差計算值。
下面用某廠生產口徑為DN80的渦街流量計為例驗證補償效果。
表3為原始檢測數據。
平均儀表常數:
Kp=(Kmax+Kmin)/2=2132.4305
非線性誤差:
δ=(Kmax-Kmin)/(Kmax+Kmin)x100%=0.62%
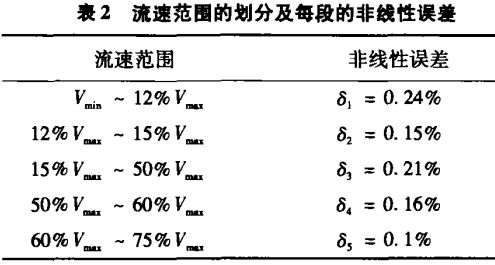
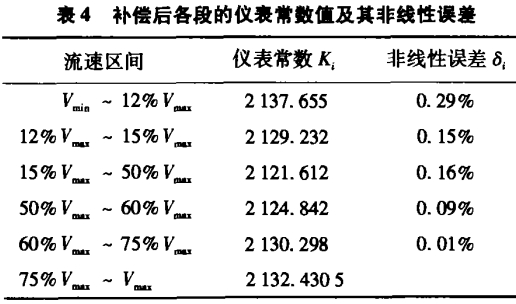
表4為補償后的各段儀表常數以及非線性誤差計算值。由此可見,補償后精度得到了提高。

4.計算流量
瞬時流量計算公式:

Q=qvt
式中:fi、Ki-----第i頻率段的漩渦分離頻率和相應的儀表常數;t---累計時間。
 |


